Another way of analysis?
When there are so many tools and techniques of prediction modelling, why do we have another field known as survival analysis? As one of the most popular branch of statistics, Survival analysis is a way of prediction at various points in time. This is to say, while other prediction models make predictions of whether an event will occur, survival analysis predicts whether the event will occur at a specified time. Thus, it requires a time component for prediction and correspondingly, predicts the time when an event will happen. This helps one in understanding the expected duration of time when events occur and provide much more useful information. One can think of natural areas of application of survival analysis which include biological sciences where one can predict the time for bacteria or other cellular organisms to multiple to a particular size or expected time of decay of atoms. Some interesting applications include prediction of the expected time when a machine will break down and maintenance will be required
How hard does it get..
It is not easy to apply the concepts of survival analysis right off the bat. One needs to understand the ways it can be used first. This includes Kaplan-Meier Curves, creating the survival function through tools such as survival trees or survival forests and log-rank test.
# install.packages("survival")# Loading the packagelibrary("survival") |
#Dataset description?pbc |
#Fitting the survival modelsurvival_func=survfit(Surv(pbc$time,pbc$status == 2)~1)survival_funcCall: survfit(formula = Surv(pbc$time, pbc$status == 2) ~ 1) n events median 0.95LCL 0.95UCL 418 161 3395 3090 3853 |
#Plot the survival modelplot(survival_func) |

As expected, the plot shows us the decreasing probabilities for survival as time passes. The dashed lines are the upper and lower confidence intervals. In the survfit() function here, we passed the formula as ~ 1 which indicates that we are asking the function to fit the model solely on the basis of survival object and thus have an intercept. The output along with the confidence intervals are actually Kaplan-Meier estimates. This estimate is prominent in medical research survival analysis. The Kaplan – Meier estimates are based on the number of patients (each patient as a row of data) from the total number who survive for a certain time after treatment. (which is the event). We can represent the Kaplan – Meier function by the formula:
1 2 | Ŝ(t)=∏(1-di/ni) for all i where ti≤tHere, di the number of events and ni is the total number of people at risk at time ti |
What to make of the graph?
Unlike other machine learning techniques where one uses test samples and makes predictions over them, the survival analysis curve is a self – explanatory curve. From the curve, we see that the possibility of surviving about 1000 days after treatment is roughly 0.8 or 80%. We can similarly define probability of survival for different number of days after treatment. At the same time, we also have the confidence interval ranges which show the margin of expected error. For example, in case of surviving 1000 days example, the upper confidence interval reaches about 0.85 or 85% and goes down to about 0.75 or 75%. Post the data range, which is 10 years or about 3500 days, the probability calculations are very erratic and vague and should not be taken up. For example, if one wants to know the probability of surviving 4500 days after treatment, then though the Kaplan – Meier graph above shows a range between 0.25 to 0.55 which is itself a large value to accommodate the lack of data, the data is still not sufficient enough and a better data should be used to make such an estimate.
Alternative models: Cox Proportional Hazard model
The survival package also contains a cox proportional hazard function coxph() and use other features in the data to make a better survival model. Though the data has untreated missing values, I am skipping the data processing and fitting the model directly. In practice, however, one needs to study the data and look at ways to process the data appropriately so that the best possible models are fitted. As the intention of this article is to get the readers acquainted with the function rather than processing, applying the function is the shortcut step which I am taking.
# Fit Cox ModelCox_model = coxph(Surv(pbc$time,pbc$status==2) ~.,data=pbc)summary(Cox_model)Call:coxph(formula = Surv(pbc$time, pbc$status == 2) ~ ., data = pbc) n= 276, number of events= 111 (142 observations deleted due to missingness) coef exp(coef) se(coef) z Pr(>|z|) id -2.729e-03 9.973e-01 1.462e-03 -1.866 0.06203 . trt -1.116e-01 8.944e-01 2.156e-01 -0.518 0.60476 age 3.191e-02 1.032e+00 1.200e-02 2.659 0.00784 **sexf -3.822e-01 6.824e-01 3.074e-01 -1.243 0.21378 ascites 6.321e-02 1.065e+00 3.874e-01 0.163 0.87038 hepato 6.257e-02 1.065e+00 2.521e-01 0.248 0.80397 spiders 7.594e-02 1.079e+00 2.448e-01 0.310 0.75635 edema 8.860e-01 2.425e+00 4.078e-01 2.173 0.02980 * bili 8.038e-02 1.084e+00 2.539e-02 3.166 0.00155 **chol 5.151e-04 1.001e+00 4.409e-04 1.168 0.24272 albumin -8.511e-01 4.270e-01 3.114e-01 -2.733 0.00627 **copper 2.612e-03 1.003e+00 1.148e-03 2.275 0.02290 * alk.phos -2.623e-05 1.000e+00 4.206e-05 -0.624 0.53288 ast 4.239e-03 1.004e+00 1.941e-03 2.184 0.02894 * trig -1.228e-03 9.988e-01 1.334e-03 -0.920 0.35741 platelet 7.272e-04 1.001e+00 1.177e-03 0.618 0.53660 protime 1.895e-01 1.209e+00 1.128e-01 1.680 0.09289 . stage 4.468e-01 1.563e+00 1.784e-01 2.504 0.01226 * ---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 exp(coef) exp(-coef) lower .95 upper .95id 0.9973 1.0027 0.9944 1.000trt 0.8944 1.1181 0.5862 1.365age 1.0324 0.9686 1.0084 1.057sexf 0.6824 1.4655 0.3736 1.246ascites 1.0653 0.9387 0.4985 2.276hepato 1.0646 0.9393 0.6495 1.745spiders 1.0789 0.9269 0.6678 1.743edema 2.4253 0.4123 1.0907 5.393bili 1.0837 0.9228 1.0311 1.139chol 1.0005 0.9995 0.9997 1.001albumin 0.4270 2.3422 0.2319 0.786copper 1.0026 0.9974 1.0004 1.005alk.phos 1.0000 1.0000 0.9999 1.000ast 1.0042 0.9958 1.0004 1.008trig 0.9988 1.0012 0.9962 1.001platelet 1.0007 0.9993 0.9984 1.003protime 1.2086 0.8274 0.9690 1.508stage 1.5634 0.6397 1.1020 2.218Concordance= 0.849 (se = 0.031 )Rsquare= 0.462 (max possible= 0.981 )Likelihood ratio test= 171.3 on 18 df, p=0Wald test = 172.5 on 18 df, p=0Score (logrank) test = 286.1 on 18 df, p=0 |
1 2 3 | #Create a survival curve from the cox modelCox_curve <- survfit(Cox_model)plot(Cox_curve) |

With more data, we get a different plot and this one is more volatile. Compared to the Kaplan – Meier curve, the cox-plot curve is higher for the initial values and lower for the higher values. The major reason for this difference is the inclusion of variables in cox-model. The plots are made by similar functions and can be interpreted the same way as the Kaplan – Meier curve.
Going traditional : Using survival forests
Random forests can also be used for survival analysis and the ranger package in R provides the functionality. However, the ranger function cannot handle the missing values so I will use a smaller data with all rows having NA values dropped. This will reduce my data to only 276 observations.
#Using the Ranger package for survival analysisInstall.packages("ranger")library(ranger)#Drop rows with NA valuespbc_nadrop=pbc[complete.cases(pbc), ]#Fitting the random forestranger_model <- ranger(Surv(pbc_nadrop$time,pbc_nadrop$status==2) ~.,data=pbc_nadrop,num.trees = 500, importance = "permutation",seed = 1)#Plot the death timesplot(ranger_model$unique.death.times,ranger_model$survival[1,], type = "l", ylim = c(0,1),) |
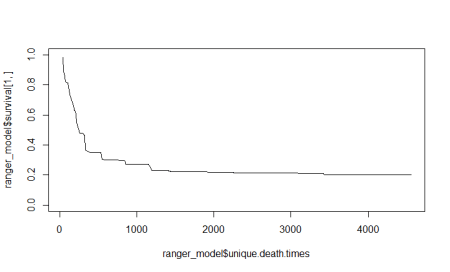
Let’s look at the variable importance plot which the random forest model calculates.
#Get the variable importancedata.frame(sort(ranger_model$variable.importance,decreasing = TRUE))sort.ranger_model.variable.importance..decreasing...TRUE.bili 0.0762338981copper 0.0202733989albumin 0.0165070226age 0.0130134413edema 0.0122113704ascites 0.0115315711chol 0.0092889960protime 0.0060215073id 0.0055867915ast 0.0049932803stage 0.0030225398hepato 0.0029290675trig 0.0028869184platelet 0.0012958105sex 0.0010639806spiders 0.0005210531alk.phos 0.0003291581trt -0.0002020952 |
These numbers may be different for different runs. In my example, we see that bilirubin is the most important feature.
Lessons learned: Conclusion
Though the input data for Survival package’s Kaplan – Meier estimate, Cox Model and ranger model are all different, we will compare the methodologies by plotting them on the same graph using ggplot.
#Comparing modelslibrary(ggplot2)#Kaplan-Meier curve dataframe#Add a row of model namekm <- rep("Kaplan Meier", length(survival_func$time))#Create a dataframekm_df <- data.frame(survival_func$time,survival_func$surv,km)#Rename the columns so they are same for all dataframesnames(km_df) <- c("Time","Surv","Model")#Cox model curve dataframe#Add a row of model namecox <- rep("Cox",length(Cox_curve$time))#Create a dataframecox_df <- data.frame(Cox_curve$time,Cox_curve$surv,cox)#Rename the columns so they are same for all dataframesnames(cox_df) <- c("Time","Surv","Model")#Dataframe for ranger#Add a row of model namerf <- rep("Survival Forest",length(ranger_model$unique.death.times))#Create a dataframerf_df <- data.frame(ranger_model$unique.death.times,sapply(data.frame(ranger_model$survival),mean),rf)#Rename the columns so they are same for all dataframesnames(rf_df) <- c("Time","Surv","Model")#Combine the resultsplot_combo <- rbind(km_df,cox_df,rf_df)#Make a ggplotplot_gg <- ggplot(plot_combo, aes(x = Time, y = Surv, color = Model))plot_gg + geom_line() + ggtitle("Comparison of Survival Curves") |

We see here that the Cox model is the most volatile with the most data and features. It is higher for lower values and drops down sharply when the time increases. The survival forest is of the lowest range and resembles Kaplan-Meier curve. The difference might be because of Survival forest having less rows. The essence of the plots is that there can be different approaches to the same concept of survival analysis and one may choose the technique based on one’s comfort and situation. A better data with processed data points and treated missing values might fetch us a better R2 and more stable curves. At the same time, they will help better in finding time to event cases such as knowing the time when a promotion’s effect dies down, knowing when tumors will develop and become significant and lots of other applications with a significant chunk of them being from medical science. Survival, as the name suggests, relates to surviving objects and is thus related to event occurrence in a completely different way than machine learning. It is important to know this technique to know more and more ways data can help us in solving problems, with time involved in this particular case. Hope this article serves the purpose of giving a glimpse of survival analysis and the feature rich packages available in R.
Here is the complete code for the article:
# install.packages("survival")# Loading the packagelibrary("survival")#Dataset description?pbc#Fitting the survival modelsurvival_func=survfit(Surv(pbc$time,pbc$status == 2)~1)survival_func#Plot the survival modelplot(survival_func)# Fit Cox ModelCox_model = coxph(Surv(pbc$time,pbc$status==2) ~.,data=pbc)summary(Cox_model)#Create a survival curve from the cox modelCox_curve <- survfit(Cox_model)plot(Cox_curve)#Using the Ranger package for survival analysis#install.packages("ranger")library(ranger)#Drop rows with NA valuespbc_nadrop=pbc[complete.cases(pbc), ]#Fitting the random forestranger_model <- ranger(Surv(pbc_nadrop$time,pbc_nadrop$status==2) ~.,data=pbc_nadrop,num.trees = 500, importance = "permutation",seed = 1)#Plot the death timesplot(ranger_model$unique.death.times,ranger_model$survival[1,], type = "l", ylim = c(0,1),)#Get the variable importancedata.frame(sort(ranger_model$variable.importance,decreasing = TRUE))#Comparing modelslibrary(ggplot2)#Kaplan-Meier curve dataframe#Add a row of model namekm <- rep("Kaplan Meier", length(survival_func$time))#Create a dataframekm_df <- data.frame(survival_func$time,survival_func$surv,km)#Rename the columns so they are same for all dataframesnames(km_df) <- c("Time","Surv","Model")#Cox model curve dataframe#Add a row of model namecox <- rep("Cox",length(Cox_curve$time))#Create a dataframecox_df <- data.frame(Cox_curve$time,Cox_curve$surv,cox)#Rename the columns so they are same for all dataframesnames(cox_df) <- c("Time","Surv","Model")#Dataframe for ranger#Add a row of model namerf <- rep("Survival Forest",length(ranger_model$unique.death.times))#Create a dataframerf_df <- data.frame(ranger_model$unique.death.times,sapply(data.frame(ranger_model$survival),mean),rf)#Rename the columns so they are same for all dataframesnames(rf_df) <- c("Time","Surv","Model")#Combine the resultsplot_combo <- rbind(km_df,cox_df,rf_df)#Make a ggplotplot_gg <- ggplot(plot_combo, aes(x = Time, y = Surv, color = Model))plot_gg + geom_line() + ggtitle("Comparison of Survival Curves") |
