Propensity scores are an alternative method to estimate the effect of receiving treatment when random assignment of treatments to subjects is not feasible.
The concept of Propensity score matching (PSM) was first introduced by Rosenbaum and Rubin (1983) in a paper entitled “The Central Role of the Propensity Score in Observational Studies for Casual Effects.”
Statistically it means…
Propensity scores are an alternative method to estimate the effect of receiving treatment when random assignment of treatments to subjects is not feasible. PSM refers to the pairing of treatment and control units with similar values on the propensity score; and possibly other covariates (the characteristics of participants); and the discarding of all unmatched units.
What is PSM in simple terms…
PSM is done on observational studies. It is done to remove the selection bias between the treatment and the control groups.
For example say a researcher wants to test the effect of a drug on lab rats. He divides the rats in two groups and tests the effects of the drug in one of the groups, which is the treatment group. The other group is known as the control group. As it is an experiment everything is controlled by the experimenter, like all these rats are genetically the same and grow up in the same environment, so he knows that any differences between them will be solely due to the drug that he has given them.
However this cannot be done with people because people are different from each other, they come in different shapes and sizes, ages, ethnicities, etc., However, at the same time people aren’t so different that we can’t find any similarities between them. This is when we can use propensity score matching.
To give an example, if a marketer wants to observe the effect of a marketing campaign on the buyers; to judge if the campaign is the only reason which influenced them to buy; he cannot deduce this as he does not know whether the people who participated in the campaign are equivalent to the people who did not participate in the campaign. There might be other influential factors that led the buyers to buy and it might not be the effect of the campaign at all. In that case he can go for a propensity score matching estimation to observe how much impact the campaign had on the buyers/non-buyers.
PSM using R…
I will now demonstrate a simple program on how to do Propensity Score matching in R, with the use of two packages: Tableone and MatchIt.
The dataset…
#Reading the raw data
> Data <- read.csv("Campaign_Data.csv", header = TRUE)
> dim(Data)
[1] 1000 4The dataset contains randomly simulated 1000 records of people with their demographic profiles, age and income, the Ad_Campaign_Response, whether they have responded to the campaign or not , 1 = Responded and 0 = Not Responded, and the Bought column, 1 = Purchased and 0 = Not Purchased.
# To view the first few records in the dataset > head(Data) Age Income Ad_Campaign_Response Bought 1 41 107 1 1 2 56 75 0 0 3 50 88 0 0 4 22 94 1 0 5 51 74 1 0 6 45 51 1 1
The Treatment and Control Population…
# The treatment population > Treats <- subset(Data, Ad_Campaign_Response == 1) > colMeans(Treats) Age Income Ad_Campaign_Response Bought 45.7500000 79.2772277 1.0000000 0.8391089 # The control population > Control <- subset(Data, Ad_Campaign_Response == 0) > colMeans(Control) Age Income Ad_Campaign_Response Bought 45.0755034 79.4832215 0.0000000 0.1107383 > dim(Treats) [1] 404 4 > dim(Control) [1] 596 4 #Here we see we have 404 treated records and 596 control records.
If we want to find out the real impact of the campaign on the purchase
> model_1 <- lm(Bought ~ Ad_Campaign_Response + Age + Income,data=Data) > model_1 Call: lm(formula = Bought ~ Ad_Campaign_Response + Age + Income, data = Data) Coefficients: (Intercept) Ad_Campaign_Response Age Income 0.2201474 0.7291988 -0.0014048 -0.0005798 > Effect <- model_1$coeff[2] > Effect Ad_Campaign_Response 0.7291988
The model above shows that the ad campaign had a 72.9% effect on the purchase.
The Propensity Scores Model…
Now let’s prepare a Logistic Regression model to estimate the propensity scores. That is, the probability of responding to the ad campaign.
> pscores.model <- glm(Ad_Campaign_Response ~ Age + Income,family = binomial("logit"),data = Data)
> summary(pscores.model)
Call:
glm(formula = Ad_Campaign_Response ~ Age + Income, family = binomial("logit"),
data = Data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.1095 -1.0208 -0.9926 1.3373 1.4521
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.6332998 0.4505631 -1.406 0.160
Age 0.0065209 0.0063705 1.024 0.306
Income -0.0006507 0.0041133 -0.158 0.874
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1349.2 on 999 degrees of freedom
Residual deviance: 1348.1 on 997 degrees of freedom
AIC: 1354.1
Number of Fisher Scoring iterations: 4
> Propensity_scores <- pscores.model
> Data$PScores <- pscores.model$fitted.values
> hist(Data$PScores[Ad_Campaign_Response==1],main = "PScores of Response = 1")
> hist(Data$PScores[Ad_Campaign_Response==0], ,main = "PScores of Response = 0")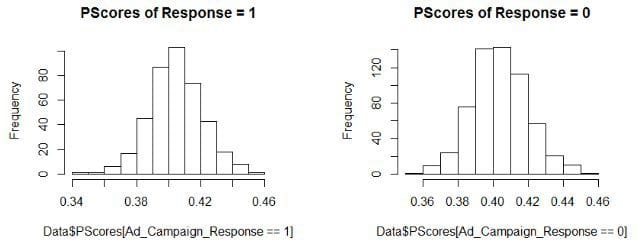
Creating a Tableone pre-matching table…
#covariates we are using
>xvars <- c("Age", "Income")
>library(tableone)
> table1 <- CreateTableOne(vars = xvars,strata = "Ad_Campaign_Response",data = Data, test = FALSE)We will use the tableone package to summarize the data using the covariates that we stored in xvars. We are going to stratify the response variable, i.e., we will check the balance in the dataset among the people who responded (treatment group) and who did not respond (control group) to the campaign. The ‘test = False’ states that we don’t require a significance test; instead we just want to see the mean and standard deviation of the covariates in the results.
Then we are going to print the statistics and also see the Standardized Mean Differences (SMD) in the variables.
> print(table1, smd = TRUE) Stratified by Ad_Campaign_Response 0 1 SMD n 596 404 Age (mean (sd)) 45.08 (10.02) 45.75 (10.33) 0.066 Income (mean (sd)) 79.48 (15.80) 79.28 (15.55) 0.013
Here we see the summary statistics of the covariates, we can see that in the control group there are 596 subjects and in the treatment group there are 404 subjects. It also shows the mean and standard deviations of these variables.
In the last column we can see the SMD, here we should be careful about SMDs which are greater than 0.1 because those are the variables which shows imbalance in the dataset and that is where we actually need to do propensity score matching.
In our example here, as it is a simulated dataset of just 1000 records and containing only 2 covariates we don’t see any imbalance but we will still go ahead with the matching and see the difference in the results.
The Matching Algorithms…
We can now proceed with the matching algorithms with our ‘pscores.model’ and the estimated propensity scores. The matching algorithms create sets of participants for treatment and control groups. A matched set will consist of at least one person from the treatment group (i.e., people who responded to the ad campaign) and one from the control group (i.e., people who did not respond to the ad campaign) with similar propensity scores. The basic goal is to approximate a random experiment, eliminating many of the problems that come with observational data analysis.
There are various matching algorithms in R, namely, exact matching, nearest neighbor, optimal matching, full matching and caliper matching. Let’s try a couple of them:
1. Exact matching is a technique used to match individuals based on the exact values of covariates.
> library(MatchIt) > match1 <- matchit(pscores.model, method="exact",data=Data) > summary(match1, covariates = T) Call: matchit(formula = pscores.model, data = Data, method = "exact") Sample sizes: Control Treated All 596 404 Matched 99 104 Discarded 497 300 Matched sample sizes by subclass: Treated Control Total Age Income 1 1 1 2 47 95 2 2 1 3 41 89 3 1 1 2 35 68 4 1 1 2 38 78 5 1 1 2 59 69 > match1.data <- match.data(match1) > View(match1.data)
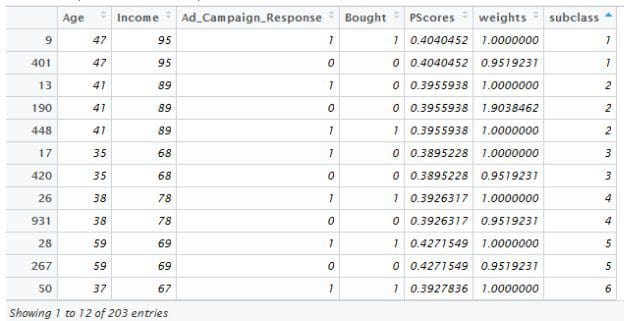
Here we can see that atleast one person in the treatment group (Ad_Campaign_Response = 1) has been matched with one person in the control group (Ad_Campaign_Response = 0).
Create the tableone for exact matching…
> table_match1 <- CreateTableOne(vars = xvars,strata = "Ad_Campaign_Response",data = match1.data,test = FALSE) > print(table_match1, smd = TRUE) Stratified by Ad_Campaign_Response 0 1 SMD n 99 104 Age (mean (sd)) 46.04 (7.57) 45.51 (7.33) 0.071 Income (mean (sd)) 79.45 (10.43) 79.82 (10.23) 0.035
We can see in the above results that there are 99 control subjects matched with 104 treatment subjects. As our sample dataset is fairly balanced we don’t see much difference in doing exact matching, instead the SMD numbers are slightly higher than the pre-matching numbers. We can try the same with nearest matching and see the effect of matching.
2. Nearest Neighbour Matching is an algorithm that matches individuals with controls (it could be two or more controls per treated unit) based on a distance.
> match2 <- matchit(pscores.model, method="nearest", radio=1,data=Data) > plot(match2, type="jitter")

> plot(match2, type="hist")
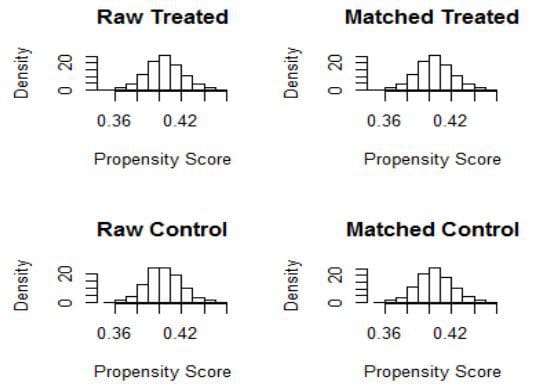
Create the tableone for nearest matching…
> table_match2 <- CreateTableOne(vars = xvars,strata = "Ad_Campaign_Response",data = match2.data,test = FALSE) > print(table_match2, smd = TRUE) Stratified by Ad_Campaign_Response 0 1 SMD n 404 404 Age (mean (sd)) 45.63 (10.26) 45.75 (10.33) 0.012 Income (mean (sd)) 79.27 (16.04) 79.28 (15.55) <0.001
The first thing we see above is that we matched 404 controls to 404 treated subjects and also we can see we get very small numbers for SMD in the covariates, hence we can conclude that we did a pretty good job of matching with nearest neighbour. We have a great balance in the dataset now to proceed with our further analysis.
Outcome Analysis (testing our hypothesis)…
We will now do a t test to test our hypothesis that there is a higher chance of purchase of the product when people respond to the ad campaign.
Before performing a paired t-test we will have to create two subsets from the matched data, one for treatment and other for control groups.
> y_trt <- match2.data$Bought[match2.data$Ad_Campaign_Response == 1] > y_con <- match2.data$Bought[match2.data$Ad_Campaign_Response == 0]
Next we will calculate a pairwise difference of the two subsets
> difference <- y_trt - y_con
Then we will perform a paired t-test on the difference, a paired t-test is just a regular t test on the difference in the outcome of the matched pairs
> t.test(difference) One Sample t-test data: difference t = 30.786, df = 403, p-value < 2.2e-16 alternative hypothesis: true mean is not equal to 0 95 percent confidence interval: 0.6835709 0.7768252 sample estimates: mean of x 0.730198
From the results above we see a very very small p-value that makes the model highly significant.
The point estimate (mean) is 0.73, that means the difference in probability of Buying the product when everyone responds to the ad campaign versus when no one responds is 0.73 ( in other words there are 73% higher chances of buying when a person responds to the ad campaign).
References:
- www.statisticshowto.com/propensity-score-matching/
- pareonline.net/getvn.asp?v=19&n=18
- rstudio-pubs-static.s3.amazonaws.com/284461_5fabe52157594320921fc9e4d539ebc2.html
- Research paper on “Propensity Score Matching in Observational Studies”.
- Inferring Causal effects from Observational data – Jason Roy
